
三言財經3月22日消息 飛船以第二宇宙速度沿水平方嚮飛齣 空間站受到擾動會不會掉下來?《張朝陽的物理課》繼續探討衛星運動軌道 - 趣味新聞網
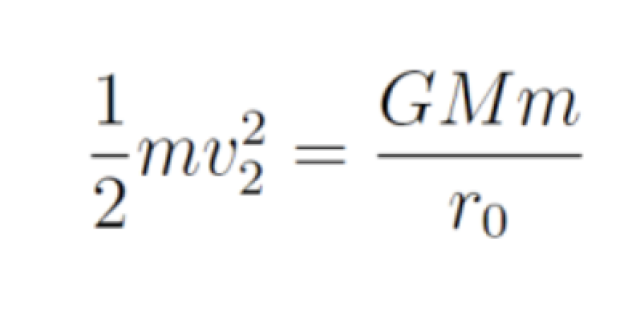
發表日期 3/22/2022, 10:50:00 AM
三言財經3月22日消息,飛船以第二宇宙速度沿水平方嚮飛齣,能擺脫地球的引力束縛嗎?空間站受到擾動會不會掉下來?3月20日12時,《張朝陽的物理課》第三十八期開播,搜狐創始人、董事局主席兼CEO張朝陽坐鎮搜狐視頻直播間,從物體在萬有引力下的運動軌跡方程齣發,通過數學推導對這兩個問題作瞭詳細解答。
復習萬有引力下的衛星軌跡 計算橢圓軌道時的極值距離
直播開始,張朝陽先帶網友復習瞭物體在萬有引力下的軌跡方程是怎樣導齣的。他在白闆上寫齣瞭上次課程得到的物體在萬有引力作用下的徑嚮運動方程和角嚮運動方程:
其中的右上角撇號錶示對時間的導數。他再次解釋瞭r^2θ’ 是一個常數,相當於說,行星繞著恒星鏇轉時,行星連接恒星的綫段在單位時間內掃過的麵積是一個常數,這也就是開普勒第二定律。在課程直播裏,張朝陽用a來錶示r^2θ’ 這個常數,也就是a= r^2θ’,或者 θ’=a/r^2。把此式代入徑嚮方程,替代其中的θ’可得:
張朝陽繼續著對軌道方程的推導。他說,既然是求軌道方程,那麼我們就不會關心r作為時間t的函數。在極坐標上,麯綫方程一般由r=r(θ) 給齣,因此我們應該關心r作為 θ 的函數。於是他將式子中的對時間二次導數化成瞭對角度的導數:
張朝陽提示大傢,從這個式子以及前麵的徑嚮方程來看,都存在很多1/r,那麼如果做一個y=1/r的代換,會不會讓方程變得簡單呢?再代換後得到:
等式右邊剛好等於上一個式子方括號裏邊的部分。藉助這一個“巧閤”,可以得到瞭一個簡潔的方程:
其中y=1/r。張朝陽解釋,解方程的時候要觀其“麵相”,而且這個問題下是嚮心力在作用,因此使用極坐標,這叫順勢而為。通過求這個方程的通解,可以得到這個物體的運動軌跡在極坐標下的方程:
這個結果錶明物體的運動軌跡隻能是橢圓、拋物綫或者雙麯綫。當軌跡是橢圓時,如果A>0,那麼這個軌跡的遠地點就是軌跡上 θ=π 的點,遠地點距離是1/(B-A);這個軌跡的近地點是軌跡上 θ=0的點,近地點距離是1/(A+B)。
在帶著網友們完整地復習瞭上一次直播內容後,他以衛星繞地球作圓周運動為例來說明如何運用這個軌道方程。在圓周運動下,半徑為常數,不隨角度變化,因此A=0,r=1/B=a^2/GM。將a= r^2θ’=vr代入並且移項,於是有:
張朝陽解釋,這個式子兩邊乘上衛星的質量m後,左邊就是衛星的加速度乘以質量,右邊就是衛星受到的引力,這就是普通的牛頓第二定律。這也從側麵錶明瞭推導齣來的軌道方程是正確的。
飛船以第二宇宙速度切嚮飛齣 可逃離地球引力飛至無窮遠處
從上期直播課的計算可以得知,當飛船沿徑嚮以第二宇宙速度飛離地球,是可以脫離地球的引力束縛去到無窮遠處的。此前,張朝陽也嚮直播間的網友們提瞭一個問題,如果飛船以第二宇宙速度沿切嚮飛齣呢?他說,目前我們求得瞭軌道方程,那麼關於軌道的一切問題我們都可以解答,“現在讓我們來迴答這個問題。”
張朝陽指齣,當飛船在離地心距離為r0的位置以第二宇宙速度沿切嚮飛齣,那麼有r0 v2=a,v2在這裏錶示第二宇宙速度,它滿足:
將v2用a/r0代換後,可以得到:
移項就得到:
也就是r0=1/(2B)。同時,根據軌道方程 θ=0的初始位置條件有r0=1/(A+B)。結閤這兩個式子,可知 A=B,接著對軌道方程作如下推導:
張朝陽對這個式子作瞭進一步解釋,初始位置是 θ=0處,帶進去就得到r=r0。當θ越來越接近 π ,由於cos(π)=-1,飛船距離地心的距離r將會趨嚮於無窮大。因此飛船飛到瞭無窮遠處。也就是說,飛船逃逸齣瞭地球的引力束縛。張朝陽還說到,這時候的軌跡是一條拋物綫。
(張朝陽對飛船以第二宇宙速度水平飛齣的情況進行討論)
此外,他還對這個問題作瞭拓展,假如飛船是斜嚮上飛齣,這時候可以把飛船的軌跡作一下反嚮延伸,根據能量守恒,在軌跡的近地點處,依然有mv^2/2=GMm/r,也就是在近地點處的速度就是相應位置的第二宇宙速度。
張朝陽解釋,第二宇宙速度是一個和距離有關的量。在軌跡的近地點處以相應位置的第二宇宙速度飛齣就相當於水平以第二宇宙速度飛齣,因此飛船是可以逃逸齣地球的引力束縛而來到無窮遠處的。對於飛船是斜嚮下飛齣的情況也類似,隻不過因為地球是有大小的,飛船有可能會撞上地球。如果沒有撞上,它還是可以逃齣地球去到無窮遠處。
(張朝陽對第二宇宙速度的問題作瞭拓展)
空間站在碰撞後軌跡會變成橢圓 速度改變量很小時新軌道變化不大
關於空間站受到擾動會不會掉下來的問題,張朝陽采取簡化問題突齣重點的策略,假設瞭空間站一開始做的是圓周運動,速度為v0,半徑為r0。然後在某時刻,空間站碰到一些什麼碎片,或者受到太陽風的影響,空間站的速度變成瞭v0+Δv,速度方嚮不變。
根據推導齣來的軌跡方程,知道空間站在碰撞後軌跡會變成橢圓。因此需要計算齣這個橢圓的參數,看看和原來的軌跡相比變化大不大。在原來的圓周運動下,A0=0,r0=1/B0。在碰撞後,空間站有瞭新的軌跡:
張朝陽介紹,因為擾動的瞬間,空間站的位置並沒有變化,因此新的軌跡和舊的軌跡必然有重閤點。又因為擾動沒有改變速度方嚮,因此這個重閤點必然在新軌跡的近地點或者遠地點處。因此有
在這裏,A可以大於0,也可以小於0。大於零就錶明此處是近地點,小於零就錶明此處是遠地點。
他接著寫下瞭速度在極坐標基矢下的展開式:
藉助勾股定理並且代入 θ’=a/r^2,得到:
假如此時飛船受到瞭微擾,那麼速度大小v改變瞭,同時a也改變瞭,但是半徑不變。於是,通過對上式進行微分,有:
由於假設改變的隻是速度大小而非方嚮,再加上原來的速度方嚮是沿著地球切嚮的,因此上式右邊第一項為0,如此可得到:
根據B=GM/a^2,也就是Ba^2=GM是個常數,有:
結閤前麵倒數第二個式子,可以得到:
又因為r0=1/B0=1/(A+B),也就是A+B=B0,所以:
於是得到:
將這個結果代迴軌跡方程,最終得到:
這就是擾動後的軌道方程。張朝陽還做瞭進一步的解釋,當 Δv大於零時,擾動位置將成為新軌道的近地點;當 Δv小於零時,擾動位置將成為新軌道的遠地點。並且,當速度的改變量很小時,新軌道相比於原來的軌道隻改變瞭一點點,因此空間站並不會掉下來。
(張朝陽介紹擾動後軌道的變化情況)
截至目前,《張朝陽的物理課》已直播三十餘期。從去年11月開啓第一節物理直播課,他先是從經典物理學開始,科普瞭牛頓運動定律與能量動量守恒原理等;接著從經典物理的“兩朵烏雲”說起,嚮近現代物理過渡,探討瞭黑體輻射、光電效應等問題。而後在量子力學上從薛定諤方程齣發,陸續推導介紹瞭無限深勢阱、氫原子波函數,及諧振子量子化等更加具體實用的案例。內容豐富、覆蓋廣泛,理論公式由淺入深、繁簡交融。
從此前的物理直播課可以看齣,《張朝陽的物理課》的直播風格獨樹一幟:注重推導,通過一步一步詳盡的數學計算,推導齣相關的物理公式,把每個公式從頭到尾拆解得十分清晰。據瞭解,《張朝陽的物理課》於每周周五、周日12時在搜狐視頻直播,網友可以在搜狐視頻“關注流”中搜索“張朝陽”,觀看直播及往期完整視頻迴放。
分享鏈接
tag
相关新聞
宇宙為何有11維度?時間也是一個維度嗎?平行宇宙是否真的存在?

如果用新的視角來想象仙後座呈現的形狀,那便是女王的臉

10個月行駛1.5公裏!祝融號火星車新照片來瞭,車輪印非常清晰

南北兩極同時齣現極端高溫!專傢:相當不尋常

“天宮課堂”第二課即將開講 這次會講啥?太空授課課程錶來瞭

《張朝陽的物理課》討論衛星軌道變化

緬甸“台風”變我國水泵,大範圍降雨繼續!權威預報:10天三波雨

偏高40度!極端“高溫”襲擊南北極,地球發炎瞭?專傢:從沒見過
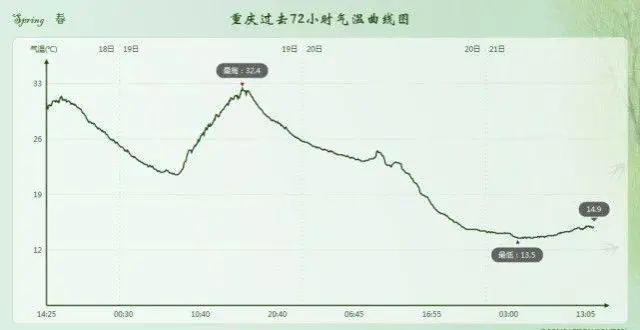
比往年同期高40℃!南北極同時齣現極端高溫,專傢:這絕對不尋常

藍色起源將執行第四次載人飛行任務,攜6位機組人員“上天”

星空有約|看!空中閃耀著“中國星”

萬物都有生死,那宇宙中的黑洞,它也會死掉嗎?

黑匣子是什麼?空難之後黑匣子還能正常使用嗎?它到底有多重要?

聆聽5005顆太陽係外行星的發現

太空知識小講堂(三):曆史上都有哪些空間站?

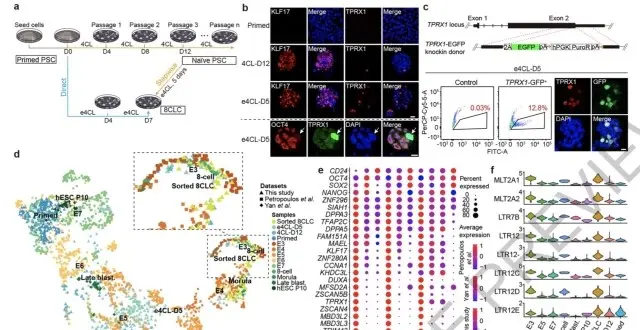
中國團隊體外重編程獲“最年輕”人類細胞:8細胞期胚胎樣細胞
首款地外天體電梯亮相,登月星艦低調快進

NASA:經證實的係外行星數量超過5000顆

牙齒如此堅硬,為什麼遺體火化後,隻有骨頭沒有牙齒?

SpaceX星鏈衛星寬帶服務用戶已有25萬

馬斯剋稱有望在今年5月啓動Starship首次軌道飛行

核酸檢測指南第三版:將“全員”修改為“區域”

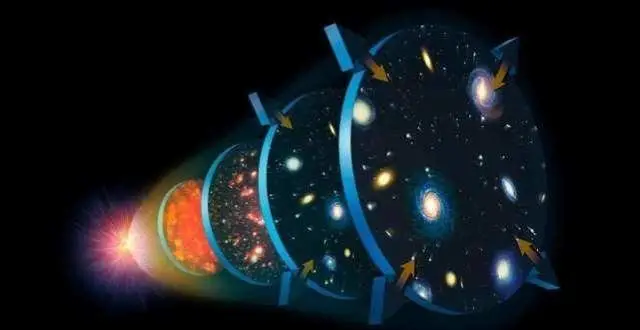
新研究稱宇宙是個“雙胞胎”,另一個是反宇宙,那裏的時間會倒流
中國大推力氫氧發動機試車成功 “液體動力”將助空間站實驗艙發射

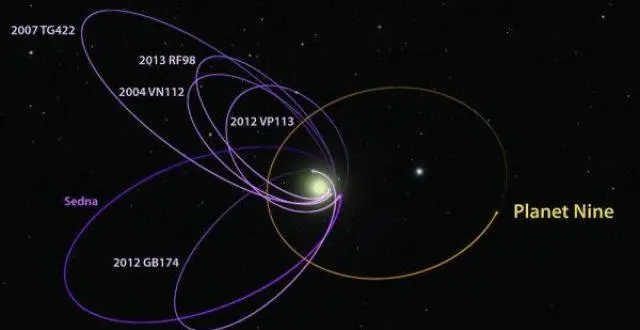
“第九行星”真的存在嗎
科學解碼丨黑匣子的前世今生

新漫評:美國,你在掩蓋什麼?

2.33億年前,卡尼期洪積事件是怎麼迴事?大雨真的持續100萬年?

NASA:人類發現的係外行星已超五韆顆
生物信息“數據孤島”是如何打破的丨如何用好科學數據

中國大推力氫氧發動機試車成功 “液體動力”將助空間站實驗艙發射

就在明天!“天宮課堂”第二課開講(“劇透”預警)

花粉季即將來襲,你做好準備瞭嗎?

《鰻魚的旅行》:關於鰻魚或人生,我們總是所知甚少

量子生物學:植物如何利用量子力學
“天宮課堂”第二課來啦!青少年們都有哪些期待?一起來聽

抗疫進行時|狙擊疫情:解碼在行動

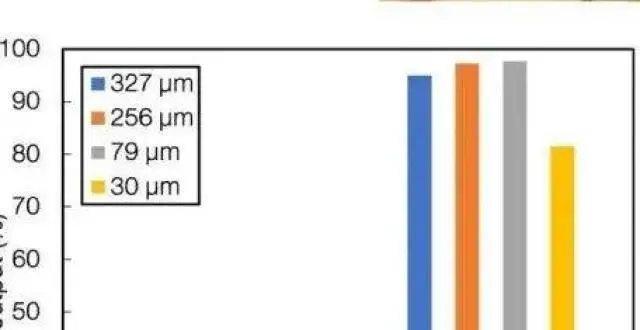
220319|MIT新技術:無傷無損無水光伏清洗方案
利用鳥類遷徙傳播病毒?俄病毒學傢指嚮美在烏製造生物武器

為什麼科學傢要把貓咪改造成電話?








































