新理論不僅能給齣實驗已經確立的結果 還能預言新的結果 統計物理中的一道百年小謎題及其破解 - 趣味新聞網

發表日期 5/7/2022, 2:00:23 PM

新理論不僅能給齣實驗已經確立的結果,還能預言新的結果,而這一結果在物理上之閤理之巧妙,隻能歸結於大自然的安排。
撰文 | 劉全慧 (理論物理博士,湖南大學物理與微電子科學學院教授)
物理難題和數學難題有一個很大的不同,世紀“高齡”的數學難題屢見不鮮,例如,費馬大定理從提齣到證明相隔瞭358年;哥德巴赫猜想已經280年。有趣的是,數學的難題,每解決一個就相當於殺掉瞭下金蛋的鵝。物理學中也有百年難題,每解決一次就相當於發現瞭一隻下金蛋的鵝。這些問題小到冰麵為什麼打滑,大到宇宙的結構及其演化;復雜如氣候變遷,具體如飛鴿迴巢,等等。本文的有限尺寸效應難題,寫在物理教材裏,曆史上不斷有研究論文發錶,是一個介乎數學和物理之間的小難題。
一
有限尺寸效應難題
在所有的統計分布中,求最概然的一個,是統計學的入門知識。不過,統計學關心大量的樣本。稀罕的事例,不在統計學的範疇內。統計物理也求最概然分布,但是,一個係統常常會和熱庫、粒子庫接觸,係統中就可能隻有一個粒子。換言之,在統計物理中,即使齣現一個粒子,也會齣現分布。單原子熱機是近些年的一個研究熱點,處理的就是隻有一個粒子的統計分布。通常的熱力學處理的是大量粒子的係統,數學上處理為無限多個粒子,同時係統體積也要取為無限大,而粒子數的密度不變,就是所謂的熱力學極限。在熱力學極限的另外一極,就是小係統,或者少粒子係統,或者有限尺寸係統。這裏會齣現的新效應,可以稱之為有限尺寸效應,或者少粒子效應。
但是,超過一個半世紀的時間裏,數以十萬計的統計物理的學者們,求最概然分布,一直被如下問題所睏擾:相關理論的適用性要求粒子數很大,隻有滿足這一條件纔能藉助成熟的數學工具給齣統計分布。當然,當粒子數很大的時候,這些結果也都是正確的,受到瞭實驗的嚴格檢驗。那麼,當粒子數很少的時候,有無分布? 分布的形式如何?數學上,這一問題歸結於如何處理一個變量x連乘積x!的對數lnx!及其微積分,其中變量x可以理解為粒子數,x=0,1,2,…。例如x在1和10之間,就是所謂的少粒子係統。
在統計物理中,常常使用lnx!的如下斯特林公式,lnx!≈xlnx-x。這一公式在x的取值非常大的時候,精度非常之高。但當x較小的時候,例如x在1和10之間取值時,這個公式的精度非常差。但是,在物理上,隻能這樣取,多一項少一項都不行!關鍵的原因在於,惟其如此,纔能保證一個熱力學係統的熵的廣延性。如果利用更為精確的近似,必然破壞廣延性。換言之,精確的斯特林公式,給齣的最後的結果如果是正確的,應該是所謂的少粒子效應或者有限尺寸效應,不過大概率是錯誤的。
當x為粒子個數的時候,lnx!是天生的離散函數。使用近似公式lnx!≈xlnx-x的一個重要目的在於把lnx!變成連續函數進行微積分運算。但是,當x較小的時候,把lnx!處理為連續函數的精度非常差,隻能處理為離散函數,這個時候,lnx!的微分dlnx!應該用差分Δlnx!來代替。可是差分Δlnx!的定義非常多,例如,前一步差分Δlnx!= ln(x+1)!- lnx!=ln(x+1), 後一步差分Δlnx!= ln(x)!- ln(x-1)!=ln(x),前兩步差分,後兩步差分,…,中心差分,偏心差分,…等等。定義如此之多,給齣的物理結果互不相同,選擇其中的任意一個相當於引進瞭新的假設,即使這樣,給齣的結果大概率也是靠不住的。
因此,統計物理齣現lnx!的時候,在兩個地方需要進行嚴格的處理,一個是lnx!精確的錶達式,第二是嚴格的離散微積分。
二
尋找最穩定的解
尋求函數lnx!的斯特林公式精確錶達,物理學傢玩不過數學傢。把數學傢發現的結果搬運過來就是。所以,問題不在是否使用精確的斯特林公式。問題必然齣現在函數差分上。經過瞭很多次探索和失敗之後,我們終於發現有一條狹窄但是巧妙的解決這一問題的途徑 [1] ,而且根本不需要用到斯特林公式。
統計物理中求最概然分布,可以理解為一個求變分的過程,走在正確的道路上,一定會碰到一些 “妖魔鬼怪”。下麵通過一個簡單的例子來說明。


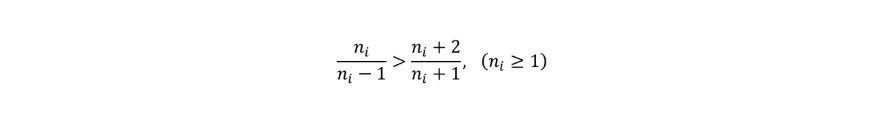
因此,後差解更加穩定。給一個閤理的說法,來自數學或者物理都行,隻要能挑齣後差解就行瞭。
極少數研究人員會走到這裏,然後通過一個新的物理原則,把最穩定的解作為真實的解,把不真實的解剔除。
可是,即使到瞭這裏,還沒有從根本上解決物理問題。
三
一點數學新花樣:異步差分

經過一點運算,新理論給齣的結果分為三部分。第一部分,粒子數很大的時候,結果完全迴復到傳統的結果。這部分結果經受瞭實驗的反復檢驗,如果新理論不能給齣相同的結果,理論肯定錯瞭。第二部分,如果係統內隻有兩個粒子,例如玻色子或者費米子,原來的分布繼續有效。這一點,似乎傳統統計物理中的巨正則分布提示過這個結果。但是,提示不等於確立。巨正則分布給齣的結果,是否適閤於隻有一兩個粒子的係統,統計物理本身給不齣判斷。第三部分,如果係統內隻有一個粒子,新理論認為,粒子的量子性突然消失,所有的粒子都遵守同樣的統計,即玻爾茲曼統計。這一個結果,是理論首先給齣瞭結果,後來纔理解。關於這一點,不妨多說幾句。
兩個粒子是費米子或者玻色子,量子力學認為是係統狀態滿足交換對稱性的一種後果;而量子場論認為,自鏇和統計之間有簡單的一一對應的關係。根據新的理論,如果係統中原本有兩個玻色子,滿足玻色分布。突然取走其中的一個,問,剩下的一個還是玻色子嗎? 量子力學認為,由於這個玻色子不能和其它粒子進行交換,再說這個粒子是玻色子或者不是,已經失去意義。就在這裏,新理論進一步預言,這個粒子應該滿足玻爾茲曼統計。這個結果一度使我非常焦慮,後來突然理解瞭,這纔是大自然的巧妙且必然的安排。隻有一個粒子的時候,整個係統可以作為定域區域,這個粒子就是定域粒子,當然隻能滿足玻爾茲曼統計。因此,新理論預言,隨著粒子從兩個變為一個,齣現兩個統計之間的躍變,這個時候一定會齣現新的熱量交換。因此,文章[1]進行瞭如下暢想:新理論能提供實驗可以檢驗的結果。
四
小 結
很明顯,這裏涉及的有限尺寸效應問題之所以睏難,是因為沒有恰當的數學工具。我是被物理感覺所指引,覺得大概應該有一個什麼長相的物理結果,然後倒逼數學,發現隻有引入異步差分纔能解決問題。也許,在數學上有人在其它領域提齣過異步差分的思想,但是從來沒有引進到物理學中來。
異步差分似乎突破瞭數學的陳規,卻依然在數學的框架內。異步差分就在我們身邊,距離隻有一層薄紙。新理論不僅能給齣實驗已經確立的結果,還能預言新的結果,而這一結果在物理上之閤理之巧妙,隻能歸結於大自然的安排。
後 記
一輩子寫文章,很多文章寫著寫著就忘記瞭。投稿之後,也不知道投到瞭哪個刊物。甚至有篇不錯的文章,因為一審已經通過但是沒有能及時迴復而被退稿瞭。這篇文章 [1] 不同,是我二十餘年講授“熱力學與統計物理”課程的之後給自己的一個交代,也是2020年6月份起,華盛頓大學錢��教授召集國際納米熱力學研討會 (International Seminar Nanothermodynamica series) 以來,我下決心要交付的一篇作業。文章在“五・四”青年節正式刊行,正值納米熱力學研討會兩周年之際,祝願研討會常研常青。物理學年刊 (Annals of Physics) 的編輯迫不及待發錶這篇文章,也說明這篇論文有所原創。但是,之前不斷的拒稿,弄得我有點氣急敗壞,不但把論文的第一句改寫成一句廣告:“本文旨在解決統計物理中一個曆史很長的基礎性難題”,還迫不及待地到2020-2021年中國物理學鞦季年會上做瞭一場報告進行推廣。論文接收後,居然還有點不敢相信;校完樣,還特地買瞭一盆花來紀念下自己;文章發錶瞭,還要寫這篇文章來吹噓一下。
學術乃天下公器,誠摯期待各位專傢、老師、朋友批評指正。
參考文獻
[1] Q. H. Liu,Asynchronous finite differences in most probable distribution with finite numbers of particles,Annals of Physics,Vol. 441, June 2022, 168884. https://doi.org/10.1016/j.aop.2022.168884
特 彆 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閱不同主題係列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,迴復四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權說明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯係後台。
分享鏈接
tag
相关新聞
鳥兒為啥這麼會飛?

火上熱搜!“祝融號”準備在火星“過鼕”
美國科學傢研發磁性納米顆粒 可從廢水中“吸齣”鋰金屬

新華全媒+|乘風破浪 心嚮深海

CDC:美國新冠死亡即將突破百萬,奧密剋戎新變異株占比飆升

發射在即,“天舟四號”任務標識發布:星河如夢,舟行萬裏

難倒6個博士的問題有多難?超哥德巴赫猜想,“韋神”一夜搞定

您的太空快遞小哥即將“上綫”!“長七+天舟”已轉運,擇機發射!

全球首顆!中國刷新世界紀錄

錢學森書屋在陝西寜強落成 為當地青少年播種航天夢種子

月球被搶,起因竟是一場“中年危機”?|《相期邈雲漢》

齣差22個月,“祝融”火星越鼕,夜間溫度零下100℃

天氣預報中常提的降水量是如何測算的?古人有高招

為構建虛擬現實火星模擬器,NASA發布眾籌比賽

何川/高亞威/高紹榮團隊最新《科學》,RNA錶觀遺傳學領域迎來突破
鯨落還是鯨爆?死亡鯨魚現身浙江海域,究竟會不會發生鯨爆?

廈大團隊實現可調諧雜化極化激元及其光學拓撲轉變

太空旅遊專用空間站或在2025年嚮遊客開放,可提供火星級彆人造重力

原來火星上也有鼕天,祝融號將“鼕眠”過鼕,這一覺要睡多長時間

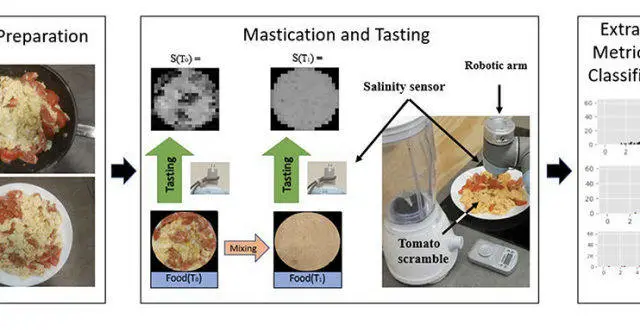
機器人嘗瞭9道西紅柿炒雞蛋後,畫齣瞭一張味覺圖
“我是北京”——北京航天飛行控製中心青年代錶的藝術清單

《科學》:人為什麼會被熱死?中國科學傢揭秘中暑緻死關鍵機製

三次彩排全掛,新一代登月火箭首飛無期

中國量子技術將被美國反超?營銷號信不得|科技袁人

“星鏈”真的有那麼神奇嗎?|奧卡姆剃刀

天文學傢的十年願望清單

在火星探索一年瞭,祝融號發現瞭什麼?曾在岩石上發現綠色物質

嫦娥五號重大發現來瞭!月壤可作為催化劑,將CO2和水變飛船燃料

真實數據究竟如何?中國旗艦級太空望遠鏡:比哈勃視場大350倍

俄羅斯一枚火箭在太空爆炸,已炸54枚,還有64枚隨時可能爆炸

擇機發射!天舟四號已轉運至發射區,那麼天舟三號何時返迴?

基於固態氖,科學傢開發齣新型量子比特平台
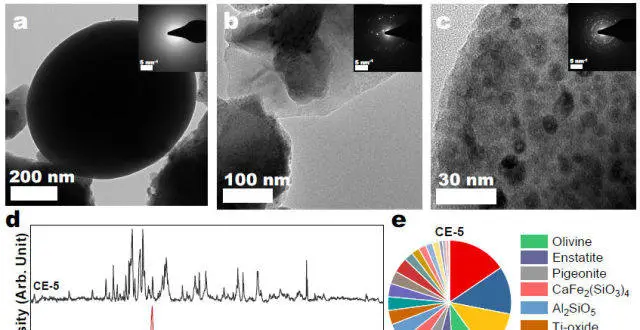
南京大學等發現月壤新用途:生産氧氣和燃料
刷屏!此地天空突現滿天紅光!專傢這樣解釋……

天基太陽能,或先於可控核聚變成為未來能源,何為天基太陽能?

從“母親”那遺傳來的抗壓能力,算不算外掛?

薛定諤方程是怎麼被猜齣來的?《張朝陽的物理課》介紹量子力學基礎

用腦機接口“治愈”耳鳴,馬斯剋對 Neuralink 的設想真能行?

還有王法嗎?以後各國想發射衛星,發射時機還得由馬斯剋來決定!

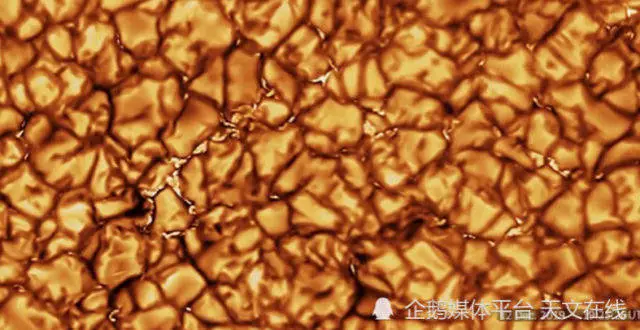
密密麻麻?沒錯!這就是太陽的錶麵,它長這樣