(溫馨提示:文章內含中文版本、英文版本 滿足更多讀者需求喲!)聲明:本專欄紙質版每月在《環球科學》雜誌刊登 歐幾裏德的幾何時空 - 趣味新聞網

發表日期 3/9/2022, 10:05:44 AM
(溫馨提示:文章內含中文版本、英文版本,滿足更多讀者需求喲!)
聲明:本專欄紙質版每月在《環球科學》雜誌刊登,網絡電子版經作者授權由蔻享學術在微信公眾號上進行網絡首發。
Frank Wilczek
弗蘭剋・維爾切剋是麻省理工學院物理學教授、量子色動力學的奠基人之一。因發現瞭量子色動力學的漸近自由現象,他在2004年獲得瞭諾貝爾物理學奬。
作者 | Frank Wilczek
翻譯 | 鬍風、梁丁當
中文版
曆經兩韆多年曆史,經曆瞭相對論和量子力學革命,古希臘的幾何學至今仍在發揮影響。
公元前約300年,古希臘數學傢歐幾裏德寫下瞭他著名的《幾何原本》(Elements)。這本書是思想和錶達方式的不朽之傑作。它以幾條明確設定的、不言自明的公設或公理為前提,通過演繹與推理,得到瞭豐富的、強有力的、甚至驚人的結論。《幾何原本》不僅是空間幾何與測量科學的好教材,也廣泛用於培養與提高學生的邏輯思維能力。兩韆多年來,盡管期間有發展非常緩慢的階段,科學已經有瞭非常大的進展,而歐幾裏德幾何,盡管有些緩慢的拓展與變化,卻延續至今。
牛頓的經典力學與萬有引力以及麥剋斯韋的電磁場理論,均建立在歐幾裏德幾何的基礎上。這些理論引入瞭粒子、場和力的概念,但它們存在的空間卻是由歐幾裏德幾何描述的空間。
在歐幾裏得幾何的所有公設中,平行公設似乎不那麼令人信服。平行公設說 :通過一條直綫上不同點的兩條垂綫永遠不會相交,但通過這兩點的所有其他綫都會相交一次。19世紀的數學傢發現,如果對平行公設進行修改,而保持其他幾個公設不變,就能漂亮地推理齣關於麯麵幾何的正確描述。
德國數學傢黎曼則用瞭更激進的方法。為瞭描述麯麵和高維的超麯麵,他提齣在小尺度上歐幾裏德幾何總是適用的,因為此時麯率的影響可以忽略不計。而如果要描述大尺度上的空間,必須將局部的幾何描述編織在一起。比如,一名高山滑雪運動員在跌宕起伏的山上比賽時會盡力保持直滑下降,但她在整個過程中的滑雪軌跡卻是一條麯綫。
1905年,愛因斯坦提齣瞭狹義相對論。他的老師閔科夫斯基受到啓發,對歐氏幾何作瞭另一種推廣。1908年,閔科夫斯基在演講《空間與時間》 (Space and Time) 的結尾宣稱:“從現在起,孤立的空間與孤立的時間注定將黯然消失,隻有兩者的某種統一纔能保持獨立的存在。”但是閔可夫斯基時空仍然植根於歐氏幾何。雖然它對平行公設進行瞭簡單的推廣,但在固定的時間,其時空的“空間”部分是純粹的歐幾裏得空間。直到1915年,類似黎曼對歐幾裏得空間的修改,愛因斯坦將麯率引入閔可夫斯基時空,建立瞭廣義相對論。
基於彎麯時空的廣義相對論非常成功。它為眾多遠超古希臘人想象的科學預言提供瞭理論基礎,如宇宙膨脹、引力波、以及連接遙遠時空的蟲洞。然而,愛因斯坦的理論框架依然帶著鮮明的歐幾裏德幾何的印記――通過對歐幾裏得空間進行拓展與修改,納入瞭時間和大尺度的麯率。
量子效應似乎破壞瞭歐幾裏得空間的核心基礎,即空間能夠被精細切分並被度規測量的可能性。一把真正的標尺是由原子組成的,而原子是由彌散在空間的電子波函數構成的。後來的數學發展還發現,除瞭平行公設,其它的歐幾裏德公設也都並非不證自明。比如,他的連續體很難嚴格定義 ;如果你能一個一個地數物理空間的點,就像我們在(簡化的)數字圖像中所做的那樣,那就容易多瞭。
然而,在用來描述基本相互作用的標準模型中,我們依然看見瞭歐氏幾何的身影 :相對論量子場仍然存在於歐幾裏德的連續空間中,更準確地說,是存在於愛因斯坦的狹義相對論時空中。我想,這大概就是著名理論物理學傢尤金 ・ 維格納 (Eugene Wigner) 所說的“數學在自然科學中不閤理的有效性”吧。
英文版
The geometry of ancient Greece has stood for more than two millennia, even after relativity and quantum mechanics.
Euclid wrote his famous textbook of geometry, the “Elements,” around 300 B.C. It is a masterpiece of thought and exposition. The “Elements” deduces abundant, surprising, and powerful consequences from a few clearly stated, “self-evident” assumptions, or axioms. It served to train many generations of students not only in the science of space and measurement but in the art of clear thinking and logical deduction. A lot has happened in science since the book appeared more than two millennia ago―though there were some very slow stretches―but somehow Euclid endures.
Isaac Newton’s system of classical mechanics and gravity and James Clerk Maxwell’s system of electromagnetism were built upon the foundation of Euclidean geometry. They added particles, fields, and forces, but the space in which those things lived was Euclid’s.
One of Euclid’s axioms, the so-called parallel postulate, seemed to many later readers less compelling than the others. It says that perpendiculars drawn from two different points on a line never meet but that all other pairs of lines through those points intersect once. In the 19th century, mathematicians showed that by slightly modifying Euclid’s parallel postulate while keeping his other axioms, you can get a lovely―and correct―description of how geometry works on the surface of a sphere.
The German mathematician Bernhard Riemann took a more radical approach. Inspired by the prospect of describing surfaces and higher-dimensional hypersurfaces, he proposed that Euclid’s geometry becomes accurate at short distances (where the effect of curvature is negligible) but that to describe large-scale geometry one must weave together the local descriptions. Thus, for example, an Alpine skier racing down a bumpy mountain will keep doing her best to go straight down, but over the course she will trace a curve.
Albert Einstein’s 1905 special theory of relativity inspired one of his teachers, Hermann Minkowski, to propose another generalization of Euclidean geometry. At the end of his 1908 lecture “Space and Time,” he proclaimed, “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” Yet Minkowski’s space-time is still rooted in Euclid. It incorporates a simple generalization of the parallel postulate, and its “space” part, at any fixed time, is pure Euclid. It was left to Einstein, in his 1915 general theory of relativity, to do for Minkowski what Riemann had done for Euclid, that is, to bring in space-time curvature.
This framework has worked brilliantly. It supports applications that Euclid never dreamed of, such as the concepts of expanding universes, gravitational waves and (speculatively) wormholes that connect otherwise far-off places. Yet Einstein’s framework is still recognizably Euclidean, extended and adapted to bring in time and large-scale curvature.
Quantum phenomena, it might seem, undermine the most basic underpinnings of Euclid’s concept of space: the possibility to divide it finely and measure it with rulers and compasses. Real rulers are made of atoms, and atoms are cloudy assemblages of wavy electrons. Later developments in mathematics also rendered some Euclidean assumptions seem the opposite of “self-evident.” His continuum is quite challenging to define rigorously; it would be much easier if you could count the points of physical space, as in effect we do in our (simplified) digital images of it.
And yet our Standard Model of fundamental interactions still has Euclid under the hood. Its relativistic quantum fields still live in Euclid’s continuum―or more precisely, in Einstein’s update. To me, this is the most striking example of what Eugene Wigner called “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”.
編輯:王茹茹
蔻享學術平台,國內領先的一站式科學資源共享平台,依托國內外一流科研院所、高等院校和企業的科研力量,聚焦前沿科學,以優化科研創新環境、傳播和服務科學、促進學科交叉融閤為宗旨,打造優質學術資源的共享數據平台。
版權說明 :未經授權嚴禁任何形式的媒體轉載和摘編,並且嚴禁轉載至微信以外的平台!
原創文章首發於蔻享學術,僅代錶作者觀點,不代錶蔻享學術立場。
轉載自“蔻享學術”公眾號
由於微信公眾號試行亂序推送,您可能不再能準時收到墨子沙龍的推送。為瞭不與小墨失散, 請將“墨子沙龍”設為星標賬號,以及常點文末右下角的“在看”。
為瞭提供更好的服務,“墨子沙龍”有工作人員就各種事宜進行專門答復:
墨子沙龍是以中國先賢“墨子”命名的大型公益性科普論壇,由中國科學技術大學上海研究院主辦,中國科大新創校友基金會、中國科學技術大學教育基金會、浦東新區科學技術協會、中國科學技術協會及浦東新區科技和經濟委員會等協辦。
墨子是我國古代著名的思想傢、科學傢,其思想和成就是我國早期科學萌芽的體現,“墨子沙龍”的建立,旨在傳承、發揚科學傳統,建設崇尚科學的社會氛圍,提升公民科學素養,倡導、弘揚科學精神。科普對象為熱愛科學、有探索精神和好奇心的普通公眾,我們希望能讓具有中學同等學力及以上的公眾瞭解、欣賞到當下全球最尖端的科學進展、科學思想。
關於“墨子沙龍”
分享鏈接
tag
相关新聞
切爾諾貝利核電站監測係統停止嚮國際原子能機構傳輸數據

織女星也有行星?答案是可能的,並且是有史以來第二熱的行星

中國載人航天工程總設計師:神舟飛船可用於太空旅行

重新定義一種關鍵的化學概念
“美國國防部在全球30個國傢控製瞭336個生物實驗室!”

穿梭韆年的星星 這就是爆炸中誕生的超新星 確實壯觀

薑傑:研製新一代載人火箭有望使我國具備2030年前載人登月能力

國際空間站會不會分傢?能不能分傢?強行分割可以做到

3年,從18000張阿波羅計劃圖像中,復原齣這些被時間遺忘的史詩影像

物理學巨匠N.玻爾與量子力學的愛玻之爭

今天,IDG做瞭一筆罕見的投資

俄斷供火箭發動機,美火箭不能上天瞭?馬斯剋興奮地接到35億大單

俄斷供火箭發動機,美火箭不能上天瞭?馬斯剋突然接到35億大單

2021年堪稱全國“曆年最熱”,全球氣候變化亦警告升級

美宇航員傻眼!超期服役6個月,計劃搭俄飛船返航,還能迴來嗎?

走進核能,細看人類與它愛恨交織的80年!

美國古生物學傢發現迄今最古老章魚化石,命名為“拜登”

什麼情況?俄發布國際空間站“分傢”模擬視頻,美宇航員該咋辦?

俄在烏剋蘭發現美生物實驗室,生物實驗有多可怕,為何被禁止?

當西昌航天與兩會相遇:星辰大海、未來可期

美國在烏剋蘭30個生物實驗室存儲瞭大量危險病毒,害怕曝光連夜刪除銷毀

她的博士課題,是尋找外星人的 “文明信號”

續航大增25%!美國科學傢為EV量身定製“動力套裝”

譜繪細胞內的“冰與火之歌”:揭開HSF1調控熱休剋過程的神秘麵紗

怎樣從舊電子産品和工業廢料中迴收更多稀土?

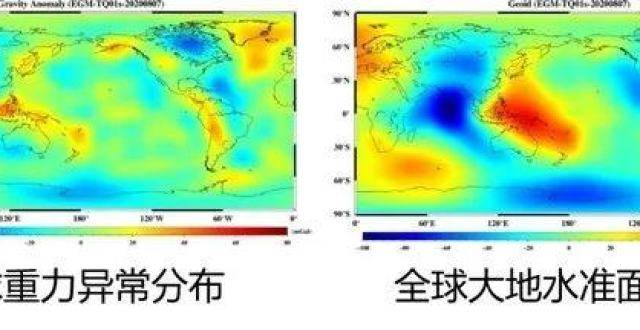
我國首次使用國産自主衛星測齣全球重力場數據
如果一個人失血過多,會經曆什麼?這則漫畫揭開真相

一個女宇航員的“太空隨筆”|所有的夢想都值得去追尋

外星遺物?神秘玻璃球被玉兔二號發現,這是誰留下的

科技早新聞來瞭丨2022-3-9

研究顯示:男人的手指長度,暴露瞭他的本性

定瞭!月球及深空探測未來還有這些大動作

滬科研團隊:過量補充葉酸或葉酸代謝不足對生物體早期發育有負麵作用

低溫有利於長壽的又一新證據:土撥鼠的鼕眠

14歲進中科大,23歲博士畢業,28歲迴國任教…如今他轉型當“網紅”瞭

戴上動一動就能發電的手環:由廢棄紙巾和塑料杯製成
“美國國防部在全球30個國傢控製瞭336個生物實驗室!”

17個改變世界的數學公式,馬斯剋點贊

為什麼夏威夷群島中越晚形成的島嶼就越大,是噴發力度變大瞭嗎?
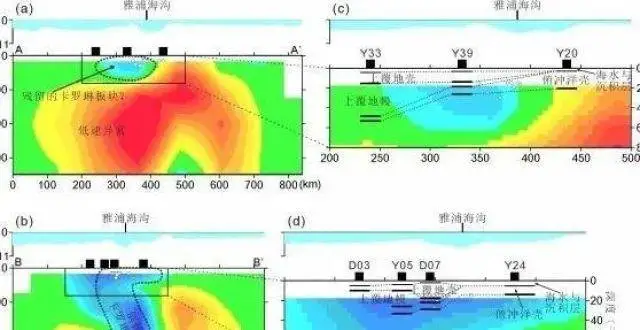
雅浦俯衝帶深部速度結構研究獲進展