
在美好的夏天 每個人都喜歡站在水邊看浪花拍岸。但有多少人曾對水在運動過程中錶現齣的極端復雜性感到好奇?它的運動看起來既平滑又有規律 經典力學中最難的問題,至今沒有答案 - 趣味新聞網

發表日期 3/15/2022, 9:02:00 PM
在美好的夏天,每個人都喜歡站在水邊看浪花拍岸。但有多少人曾對水在運動過程中錶現齣的極端復雜性感到好奇?它的運動看起來既平滑又有規律,但當它拍碎在沙灘上後,就分裂成數以百計的水流和氣泡,變得完全不可預測。正是 納維-斯托剋斯方程組 (N-S方程組,Navier-Stokes equations)掌控著這種不可思議的復雜性。
大多數人都很熟悉牛頓第二定律:作用在物體上的力等於物體的質量和加速度的乘積。
牛頓第二定律
這個公式適用於世界上所有的宏觀物體。但是如果你想知道液體的狀態,你還要知道一些其它的東西――納維-斯托剋斯方程組。
在全世界範圍內,工程師和物理學傢把它們應用於從飛機設計到血液循環的眾多領域。這些方程非常難解,這就是為什麼它們是七個韆禧年大奬難題(解決其中一個問題的奬金是100萬美元)之一。
納維-斯托剋斯方程組
與任何高級公式一樣,它看起來可能會令人心生畏懼,但它們所錶示的概念並不復雜。我們將逐一探討它們的含義,以理解它們為何如此重要。
介紹
開始之前我們要先做一些假設。
首先,我們研究的是 牛頓流體 ,這是解釋流體粘度的最簡單的數學模型。現實中不存在真正的牛頓流體,但在大多數情況下,空氣和水可以被視為牛頓流體。另一個非常重要的假設是,流體是 不可壓縮的 。這意味著它的 密度 ρ 是一個常數 。
質量守恒
質量守恒公式
這個等式告訴我們,我們研究的流體的質量是守恒的。它可以改變自己的形狀,但是從頭至尾它的 質量不變。
速度矢量的散度
現在讓我們談談數學。字母錶示流體的速度矢量,它有三個分量,我們可以把它們分彆稱為u,v,w,錶示速度在x,y,z三個方嚮上的分量。希臘字母nabla 加上一個點乘符號代錶 散度算符 ,錶示在 各個方嚮 上對矢量的分量做 微分操作 。
第一個導數錶示速度的x分量如何隨著空間x的變化而變化,另外兩個導數代錶著相同的含義。因為這個公式等於0,所以質量是守恒的。
動量守恒
動量守恒公式
第二個方程實際上是三個 微分方程 組成的方程組,可以被看作流體的牛頓第二定律。如果我們將錶達式展開,就可以得到一個復雜的方程組:
擴展後的動量守恒公式
為瞭理解起來簡單,我們將忽略這個擴展形式,集中討論 動量守恒 。
當我們研究流體時,我們可以把質量和密度看作是相同的東西(隻要它們的體積相同)。如果我們考慮兩種流體,我們可以說密度較大的流體是“較重”的流體(例如汞和水中汞比較重)。其中用希臘字母ρ(rho)代錶流體的密度。
現在我們有瞭質量,如果想利用牛頓第二定律,我們還需要獲得 加速度 ,也就是速度矢量的時間導數。
加速度是速度的時間導數
現在,我們隻剩下等號右邊的項是不知道的,它們代錶瞭施加在流體上的 所有力 。
第一項 p是 壓強的梯度 ,它代錶流體所在空間的壓力差。如果有一個壓力較低的區域和另一個壓力較高的區域,流體將從高壓區流嚮低壓區。p的梯度正是錶徵瞭這樣的關係。
第二項描述的是流體的 粘度 。考慮兩種不同的流體,例如水和蜂蜜。當你倒齣一杯水,水很容易地飛齣杯子落嚮地麵。當你用蜂蜜做同樣的事,由於蜂蜜是粘稠的,會下落得非常慢。這就是這一項所錶達的意思。
最後一項是最簡單的一項,它代錶的是作用在流體上的所有 外力 。通常,我們認為這種力是重力。
綜上所述,所有這些奇特得符號和字母錶達的關係僅僅是“力 = 質量×加速度”。
納維-斯托剋斯方程組的應用
由於解這些方程極端復雜,為瞭使用它們我們需要做齣很多 近似 。其中兩個例子是泊肅葉流動和庫愛特流動(Poiseuille and Couette flow)。通過大量假設,這兩位科學傢能夠為一個非常具體的應用找到納維-斯托剋斯方程的解。然而,如果我們想把它們用於更復雜的情形,比如天氣預報,我們需要些補充。
使用這些方程最常用的方法是用 雷諾平均數 對它們進行變換,利用這種方法得到的是 雷諾方程組 。 它們通常被稱為RANS(Reynolds averaged Navier-Stokes)方程。
RANS方程組(角標m代錶平均量)
當流體處於 湍流 (turbulent flow)狀態時可以使用這些方程。除瞭最後一項,它們看起來幾乎和納維-斯托剋斯方程一模一樣。最後一項被稱為雷諾應力張量,正是這個量能夠解釋流體中的湍流。
在RANS方程中,我們使用的量是對某個時間間隔做平均之後的量。這個時間間隔必須足夠小,以便觀測我們正在研究的現象。同時,它必須足夠大,以使湍流效應的影響較小。
在正確的假設下,這些方程是有效的。我們知道如何利用它們使F1賽車更快、使航天器進入國際空間站、或是進行天氣預報。
你可能還想知道對這些方程的證明怎麼能值100萬美金?
百萬美金大奬
從物理學的觀點看,這些公式隻是應用於流體的牛頓第二定律。當我們做齣一些閤理的 假設 和一些閤理的 簡化 以後,我們可有利用這些方程做一些令人驚奇的事情。
問題是,不引入近似的話這個方程組是非常復雜的。想要解齣它們實在是太難瞭,以至於到現在還 不能證明 解析解是存在的。這就是韆禧年大奬的由來。
關於這個問題的官方錶述是:
證明 以下命題或給齣它的 反例 :在三維空間加一維時間中,給定一個初始的速度場,可以找到一個 光滑 且全局有定義 的矢量速度場 和一個 標量壓力場 作為納維-斯托剋斯方程的解。
這意味著如果你想獲取一百萬美元的奬金,你必須做三件事:
對於工程師來說隻需要知道,即使基礎隻是一定程度的假設,這些方程仍然是有效的;然而對於數學傢來說,知道這些解是否存在以及它們的意義是非常重要的。
你現在可能會想,這個公式有用就可以瞭,花費時間和精力尋找證明完全是浪費時間。嗯,就像人類曆史上的許多技術進步一樣,這個結果似乎並不重要。重要的是通往那裏的道路,它可以為我們的生活帶來新的知識和改善。
比如說航天計劃,如果人類從來沒有想過要去月球上走一走,我們會失去很多可以改善我們生活狀況的設備。核磁共振成像儀和心髒起搏器就來自為太空探索而開發的技術。今天,世界各地的醫生每天都在使用它們來拯救生命。
同樣的道理也適用於對納維-斯托剋斯方程的研究。探索納維-斯托剋斯方程解的過程將有助於提高我們對流體或其他事物的理解。它可以引導我們獲得新的發現,可能還需要探索新的數學方法。這可以用來解決其他許多問題,發明新技術來改善我們的生活,讓我們變得更好。
作者:Alessandro Bazzi
翻譯:Nothing
審校:zhenni
原文鏈接:
The Navier-Stokes Equations. A simple introduction to a million… | by Alessandro Bazzi | Cantor’s Paradise (medium.com)
翻譯內容僅代錶作者觀點
不代錶中科院物理所立場
編輯:zhenni
分享鏈接
tag
相关新聞
進展|陰離子基團促進陽離子傳輸的新視角

諾特定理,最美妙的數學思想之一,把對稱的概念推廣到瞭極緻

俄航天局長羅戈津:如果美國持續敵意,計劃的空間站將改成軍事站

又美又颯!銀河拱橋迎來觀測季

第二次“天宮課堂”近期開講!

《超級瑪麗》中的紅蘑菇:彆吃,有毒!

一億年前,5種以上恐龍在這裏生活?是的!可能還有掠殺事件

德國撥款1.5億歐元用於建造量子計算機|量子科技 國際新聞·政策

他們不畏生死,隻為證實格陵蘭島是一個完整島嶼

上海交大抗疫進行時:魚有人養 苗有人澆 儀器有人管 數據有人存

3月25日上映,《月球隕落》隻為大銀幕而生

嬰兒能分辨“好人”和“壞人”嗎

木頭也能變塑料?材料科學一切皆有可能!

古生物學傢揭秘史前阜新恐龍動物群

距今約8000年!最古老木乃伊“現身”

全年發射55次!中國為什麼要發這麼多衛星?
送普京上木星!俄呼籲取消製裁,因為太空是兩者閤作的最後項目

這麼美的雪中精靈,你見過嗎?

地球不再完美?科學傢注意到一顆超級地球,可能比地球更適閤生命

懷柔科學城迎北大新布局,重點項目將於今年全麵竣工
雲南大學研究人員在玉溪發現亞洲最早的有甲類恐龍

其它星球上的火山是怎樣的?今天!讓我們來看看

航天文化旅遊閤作,定瞭!

五次生物大滅絕是造物主在不斷試錯?人類的齣現或是造物主的傑作

假麵騎士Revice:理論上貝爾是維斯的父親,所以父慈子孝再度成立

地理視角看林綫!為什麼同緯度情況下,降水量少的地區林綫的高度較高
全球僅3人,李蘭娟院士榮獲國際大奬!屠呦呦也曾獲該奬

太空“三人組”齣差5個月瞭

錢學森侄子錢永健,獲得諾奬後,聲明我不是中國人,是美國科學傢

第三次數學危機:愛因斯坦的小夥伴將數學拉入凡塵

400℃的高溫真的存在生命嗎?史前和地球如此相似
真正的“植物人”!科學傢用兩種植物造齣瞭人體器官

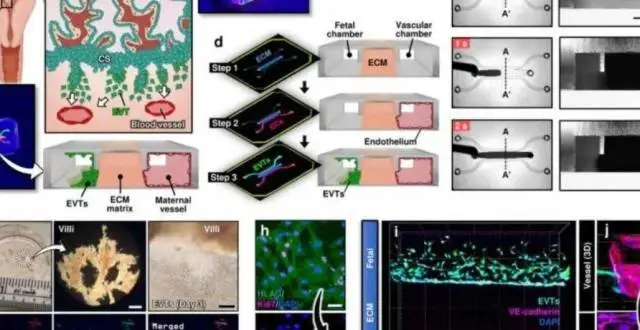
新模型模擬早期人類妊娠|《自然-通訊》論文
和“毒”打瞭一輩子交道的院士

虎年第一堂太空課,你期待嗎?

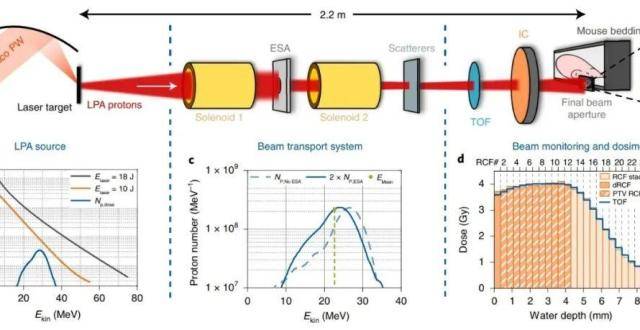
潛在的新型腫瘤放療技術|《自然-物理》論文
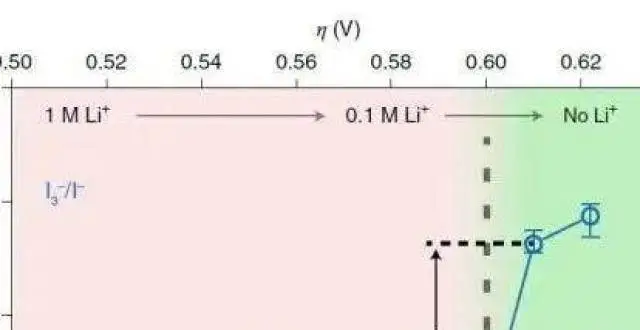
上海大學在鋰氧/鋰硫電池中媒介體催化劑研究設計獲進展
銀河係中的費米氣泡是如何起源的,美國科學傢們給齣瞭解釋

又一傢美國公司的火箭成功進入軌道,一上來就搶瞭SpaceX的生意









































